FIGURAS CÓNICAS Y CORTES EN EL CONO
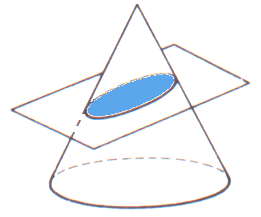
Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.
La generatriz es una cualquiera de las rectas oblicuas.
El vértice es el punto central donde se cortan las generatrices.
Las hojas son las dos partes en las que el vértice divide a la superficie cónica de revolución.
Se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas.
Secciones cónicas:
ECLIPSE
La elipse es la
sección producida en una superficie cónica de revolución por un plano
oblicuo al eje, que no sea paralelo a la generatriz y que forme con el
mismo un ángulo mayor que el que forman eje y generatriz.
α < β <90º
La elipse es una curva cerrada.
La elipse con centro (0, 0) tiene la siguiente expresión algebraica: 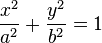
CIRCUNFERENCIA
La circunferencia es la sección producida por un plano perpendicular al eje.
β = 90º
La circunferencia es un caso particular de elipse.
PARÁBOLA
La parábola es la sección producida en una superficie cónica de revolución por un plano oblicuo al eje, siendo paralelo a la generatriz.
α = β
La parábola es una curva abierta que se prolonga hasta el infinito.
HIPÉRBOLA
La hipérbola es
la sección producida en una superficie cónica de revolución por un plano
oblicuo al eje, formando con él un ángulo menor al que forman eje y
generatriz, por lo que incide en las dos hojas de la superficie cónica.
α > β
La hipérbola es una curva abierta que se prolonga indefinidamente y consta de dos ramas separadas.
Por el teorema de
potencia de un punto:
 .
.
Al ser
PM paralela a
AC, los triángulos
HVP,
HKA y
BCA son semejantes y así:
 .
.
Usando nuevamente los paralelismos:
 .
.
Despejando
HV y
VK para sustituir en la fórmula de
QV² resulta en
 .
.
Pero el valor de

es una constante pues no depende de la posición de
V, por lo que haciendo

arroja la expresión moderna
y =
ax2.
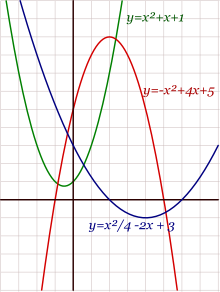
Parábolas verticales, con ecuaciones de la forma y=ax²+bx+c.
Aplicando una sustitución de coordenadas podemos obtener ahora la
ecuación de una parábola vertical para cualquier posición de su vértice.
 por su radio al cuadrado:
por su radio al cuadrado:  por su radio al cuadrado:
por su radio al cuadrado: 


 , de una esfera se expresa en función de su radio
, de una esfera se expresa en función de su radio  como:
como:




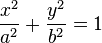



 .
. .
. .
. .
. es una constante pues no depende de la posición de V, por lo que haciendo
es una constante pues no depende de la posición de V, por lo que haciendo